How To Find The Area Of A Half Circle

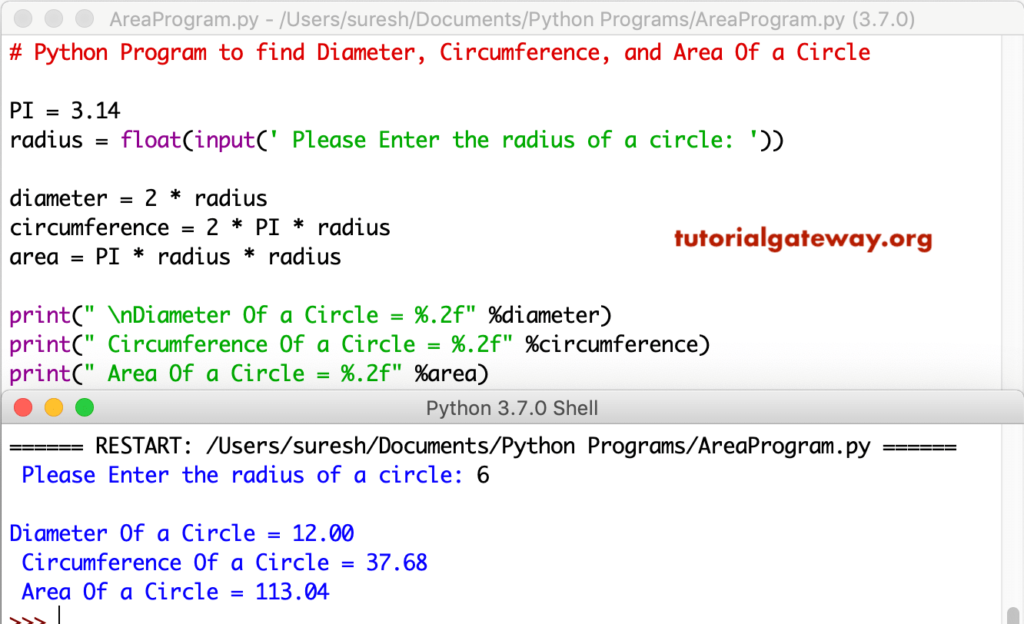
Let's jump to number one on our area of a semicircle worksheet. In this case we are given the distance from the middle of the circle to the outer edge which is known as the radius. We know that the radius is equal to 6 inches because it's given to us in order to solve using the formula. We're going to take our radius which is 6 inches and substitute it in for r into the formula. We take area equals pi times the radius which in this case is 6 squared and then divided by 2.

First thing we do according to order of operations is 6 squared so 6 times 6 which is 36 and then we're going to divide by 2. The Area of a Semicircle is all of the area that is inside of a semicircle. The way you find the Area of a Semicircle is similar to how you find the area of a circle. Usually you find the area of a semicircle using radius but sometimes you will have to find the Area of a Semicircle with diameter.

The diameter is twice as long as the radius, or the radius is half of the diameter. The formula for how to find Area of a Semicircle is area equals pi times the radius squared then divided by two. If you have the area of a semicircle with diameter that means that you have to divide the diameter by two to get the radius.

Once you have the radius you can use the Area of a Circle formula. When simplifying you need to do follow the order of operations. You must square the radius and then multiply it times pi and then finally divide by two.

So far, we have found area for rectangles, triangles, trapezoids, and circles. An irregular figure is a figure that is not a standard geometric shape. Its area cannot be calculated using any of the standard area formulas. But some irregular figures are made up of two or more standard geometric shapes. To find the area of one of these irregular figures, we can split it into figures whose formulas we know and then add the areas of the figures. The next problem on our area of a semi-circle worksheet we're going to talk about how to find the area of a semi-circle with diameter.

We know that the area of a semi-circle is pi times the radius squared and then divided by 2. To get the radius all you do is you take the diameter divide by 2. So 3 divided by 2 is 1.5 feet so now we know the radius is 1.5 and then you follow the same procedure that you did in the previous problem. You take the radius which is 1.5 and you substitute it in where r used to be. Area is equal to pi times the radius which is 1.5 squared and then you're going to divide it by 2.

The only extra step in finding the area of a circle with the diameter is having to divide the diameter by 2 to get the radius. Πr² is the formula for finding the area of a circle. To find the area of a semicircle just divide the answer by two. So take the radius, square it, which in this case would be 100, multiply it by π [pi (3.14)] and divide it by two.

The Area of a Semicircle is the area that is within a semicircle. Typically you discover the area of a semicircle by utilizing the radius of the semicircle, however you can discover the Area of a Semicircle with diameter. The diameter is twice the length of the radius, in other words, the radius is half of the diameter. The equation for how to discover Area of a Semicircle is pi times the radius squared divided by two equals the area. In the event that you have to find the Area of a Semicircle with diameter you have to divide the diameter by two. Then you can utilize the Area of a Semicircle equation.

We also know that a segment formed from the midpoint of the semi circle to the upper right vertex of the square is also the radius of the semi circle. Therefore, it is possible to form a right triangle and generate another expression for the radius based on the Pythagorean theorem. The picture of the radius is illustrated below. If the area of the circle is not equal to that of the triangle, then it must be either greater or less.

We eliminate each of these by contradiction, leaving equality as the only possibility. We use regular polygons in the same way. Circles can be halved along their diameter to form two semicircles. Calculate the perimeter and area, and also determine the diameter and radius of a semicircle using the provided formulas. Find out what's the height, area, perimeter, circumcircle and incircle radius of the regular triangle with this equilateral triangle calculator.

Here, we have discussed the programs to find the area and perimeter of semicircle in C, C++, Java, C#, PHP, python, and JavaScript. Hope you find the article helpful and informative. It is more generally true that the area of the circle of a fixed radius R is a strictly decreasing function of the curvature. The area of a regular polygon is half its perimeter times the apothem.

As the number of sides of the regular polygon increases, the polygon tends to a circle, and the apothem tends to the radius. This suggests that the area of a disk is half the circumference of its bounding circle times the radius. Term Definition Area Area is the space within the perimeter of a two-dimensional figure. Circle A circle is the set of all points at a specific distance from a given point in two dimensions.

Diameter Diameter is the measure of the distance across the center of a circle. The diameter is equal to twice the measure of the radius. In either case, finding the perimeter or the area of the quarter circle starts with knowing the circle formulas themselves. We know that the radius of a quarter circle is the same as the radius of the whole circle. That is, it is equal to the radius r that was used in the formula for the circumference. We will break the figure into a rectangle and two semi-circles.

The area of the figure will be the sum of the areas of the rectangle and the semicircles. The given figure is irregular, but we can break it into two rectangles. The area of the shaded region will be the sum of the areas of both rectangles. In either case, the cross-section is the same all the way through, like the cylinder. The volume of the prism is the area of the base times the height. So to calculate height, divide the volume of a prism by its base area.

Forget conventional ways of solving math questions. In DS, Variable approach is the easiest and quickest way to find the answer without actually solving the problem. Remember equal number of variables and independent equations ensures a solution. A semicircle is a one-dimensional locus of points that forms half of a circle. The full arc of a semicircle always measures 180°. In mathematics, a semicircle is a one-dimensional locus of points that forms half of a circle.

The area of a semicircle is half the area of the circle from which it is made. Any diameter of a circle cuts it into two equal semicircles. In the below figure, the line AC is called the diameter of the circle. The diameter divides the circle into two halves such that they are equal in area.

These two halves are referred to as the semicircles. The area of a semicircle is half of the area of a circle. The two endpoints of the semicircle's diameter and the inscribed angle will always form a right triangle inside the semicircle.

Area Of A Half Circle Formula Calculator The angle inscribed in a semicircle is always 90°. The inscribed angle is formed by drawing a line from each end of the diameter to any point on the semicircle. It doesn't matter which point on the length of the arc, the angle created where your two lines meet the arc will always be 90°. The area of a semicircle is always expressed in square units, based on the units used for the radius of a circle.

The area of a semicircle is the space contained by the circle. The area is the number of square units enclosed by the sides of the shape. The tool works as semicircle perimeter calculator as well - e.g., if you want to braid the rug, you can calculate how much lace you'll need.

In our case, the perimeter equals 10.28 ft. The rectangle has a length of 105[/latex] m and a width of 68[/latex] m. The semi-circles have a diameter of 68[/latex] m, so each has a radius of 34[/latex] m. Moving the slider changes the height of the horizontal line and the area of the shaded region. The answer box shows the shaded area at any time. The plot displays the relationship between the shaded area and the central angle.

To find arc length, start by dividing the arc's central angle in degrees by 360. Then, multiply that number by the radius of the circle. Finally, multiply that number by 2 × pi to find the arc length. A semicircle is a half circle, formed by cutting a whole circle along a diameter line, as shown above. When a line passes through the center and touches the two ends of the circle, then a semicircle is formed.

The diameter of a circle divides it into two halves that are referred to as semicircles. A semicircle is the half part of a circle. But before writing the programs, let's first see a brief description of the semicircle and the formulae to find its area and perimeter.

In this article, we will discuss the program to find the area and perimeter of semicircle in different programming languages. We can stretch a disk to form an ellipse. Because this stretch is a linear transformation of the plane, it has a distortion factor which will change the area but preserve ratios of areas. This observation can be used to compute the area of an arbitrary ellipse from the area of a unit circle. We have seen that by partitioning the disk into an infinite number of pieces we can reassemble the pieces into a rectangle.

This is called Tarski's circle-squaring problem. The nature of Laczkovich's proof is such that it proves the existence of such a partition but does not exhibit any particular partition. For, a perpendicular to the midpoint of each polygon side is a radius, of length r.

And since the total side length is greater than the circumference, the polygon consists of n identical triangles with total area greater than T. Again we have a contradiction, so our supposition that C might be less than T must be wrong as well. The triangle has a base of 5.5 inches and a height of 4 inches. The diameter of the circle matches the base of the triangle. The triangle has a base of 7 inches and a height of 6 inches.

The triangle has a base of 5 inches and a height of 4 inches. Next, recognize that you have been given a diameter and need to divide that by 2 to get the radius. The problem states that the diameter of the circle is the same as the width of the rectangle, 3 feet.

Here you will find a range of free printable area sheets and support, which will help your child to learn to work out the area of different semi circles. This inscribed angle is formed by drawing a line from each end of the diameter to any point on the semicircle. The perimeter of a quarter circle is a little trickier. It includes two segments that are the radius of the quarter circle, added with the curved part that is the outside of the circle. How to Find the Area of a SemicircleTo find the area of a semi-circle, you need to know the formula for the area of a circle. This is because, a semi-circle is just the half of a circle and hence the area of a semi-circle is the area of a circle divided by 2.

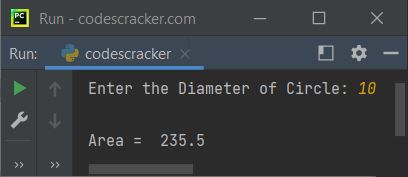
The area of a semi-circle with radius r, is (πr2)/2. Π is a constant which is approximately 3.14 or 22/7. Okay, what about a semicircle with a 10-foot diameter?

We need the radius of our area formula, but this diagram gives us the diameter. Remember from earlier, though, that the radius of a circle is half its diameter. So in this case, the radius is 10/2, or 5 feet long. Now, we can plug values into our formula. The perimeter of a semicircle is half the original circle's circumference, C, plus the diameter, d. To find the area of a semicircle with diameter, divide the diameter by 2 to find the radius, and then apply the area of a semicircle formula.

Remember to state your answer in units squared. Since you're finding the area of a shape, you'll have to use units square d in your answer to indicate that you're working with a two-dimensional object. A high school track is shaped like a rectangle with a semi-circle on each end. The rectangle has length 105[/latex] meters and width 68[/latex] meters. Find the area enclosed by the track. Round your answer to the nearest hundredth.